Scientific Papers

Performance of Automatic Active Space Selection for Electronic Excitation Energies
Authors: Reza G. Shirazi, Alexander Zech, Peter Pinski, Vladimir V. Rybkin
Computation of electronic spectra is one of the most important applications of methods capturing static electron correlation, including complete-active-space self-consistent field (CASSCF) and post-CASSCF theories. Performance of these techniques critically depends on the active space construction, both in terms of accuracy and computational effort. In this work we benchmark the performance of automatic active space construction, as implemented in the Active Space Finder software, for the computation of electronic excitation energies. The multi-step procedure constructs meaningful molecular orbitals and selects the most suitable active space based on information from more approximate correlated calculations. It aims to tackle a key difficulty in computing excitation energies with CASSCF: choosing active spaces that are balanced for several electronic states. The Active Space Finder is tested with several established data sets of small and medium-sized molecules and shows encouraging results. We evaluate multiple setting configurations and provide practical recommendations.
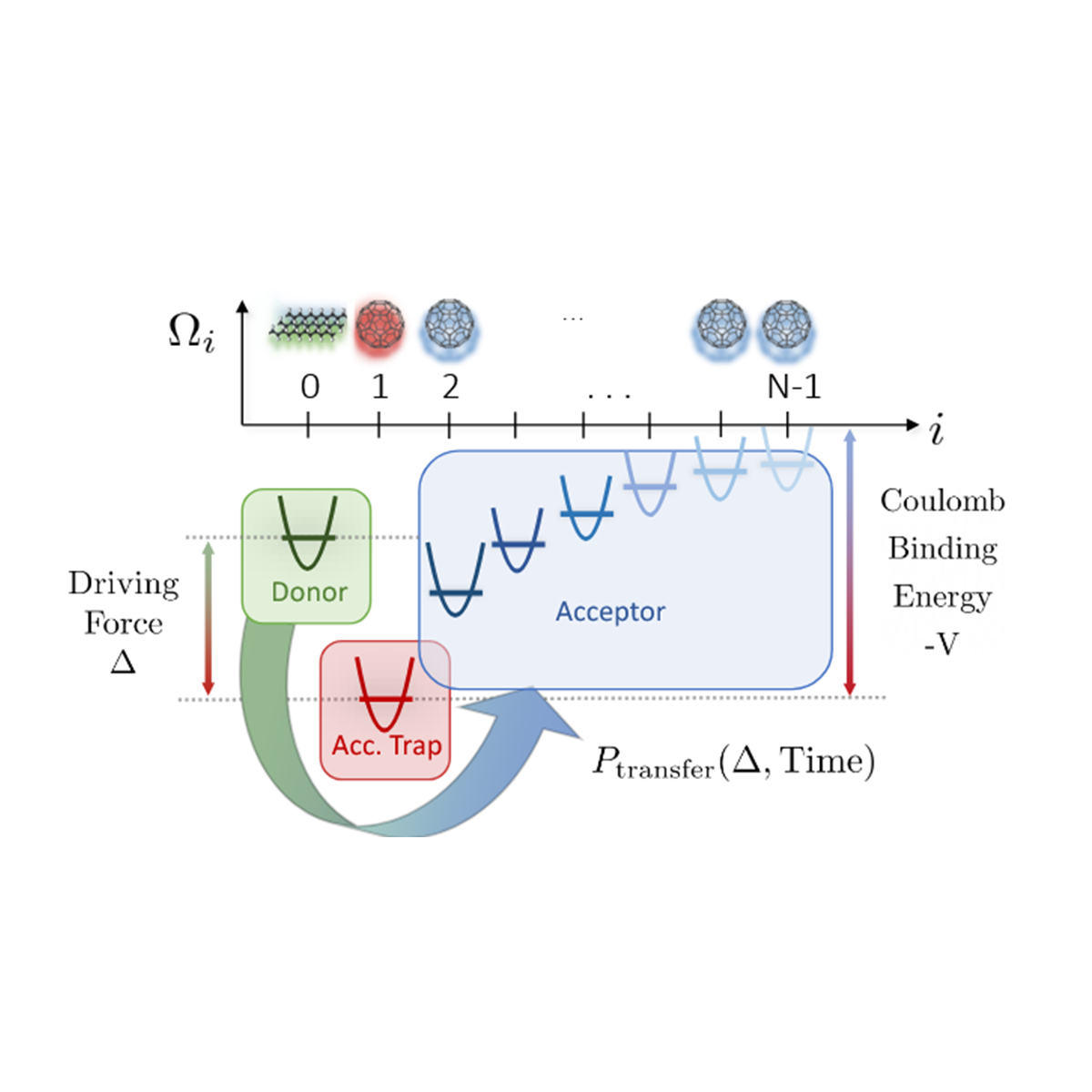
Simulating Electron Transfer on Noisy Quantum Computers: A Scalable Approach to Open Quantum Systems
Authors: Marvin Gajewski, Alejandro D. Somoza, Gary Schmiedinghoff, Pascal Stadler, Michael Marthaler, Birger Horstmann
Simulating large electronic networks with vibrational environments remains a fundamental challenge due to the long lifetimes of electronic-vibrational (vibronic) excitations on the picosecond scale. Quantum computers are a promising platform to simulate the dynamics of open quantum systems aided by intrinsic hardware-noise, with successful demonstrations of models with two electronic sites. We simulated a microscopic model of electron-transfer (ET) with a single donor and up to nine acceptor sites on a superconducting processor of IBM, using a model-specific error mitigation scheme. Our results using up to 20 qubits reveal a probability of ET that is well aligned with classical calculations where electronic and vibronic transfer resonances can be identified at the expected driving forces. We conducted 10 independent experiments per system size on different days, accounting for hourly fluctuations in error rates. We find that the most important ingredient for large-scale simulations is a large number of available qubits connected by high-fidelity gates, with coherence times above the threshold set by the target open system. Because the vibronic mechanism of electron transfer is entanglement-driven, our simulation is a natural application-based benchmark, in which the hardware capacity to produce and sustain entanglement is quantified by the maximum system size for which the hardware produces accurate results.
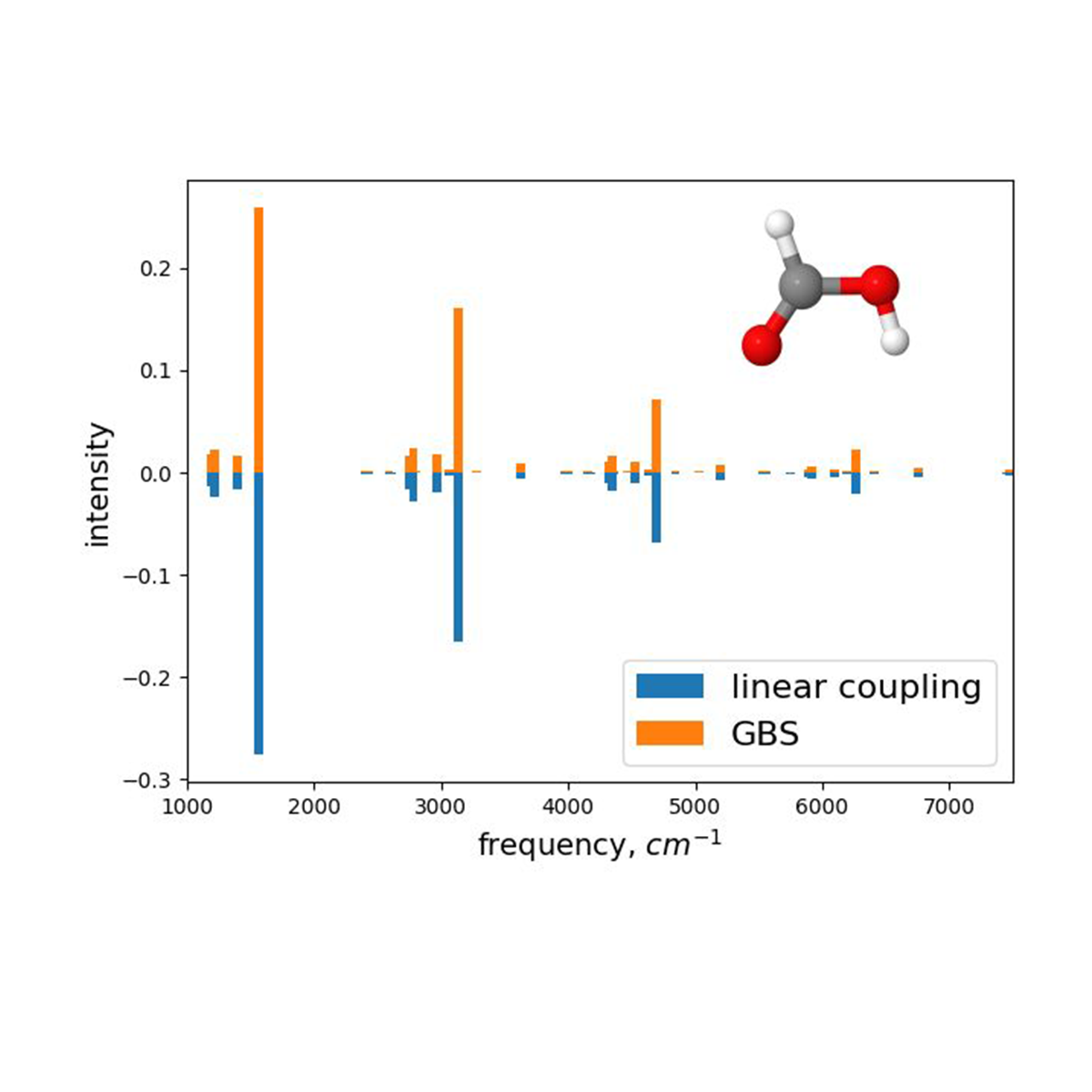
Is the Full Power of Gaussian Boson Sampling Required for Simulating Vibronic Spectra Using Photonics?
Authors: Jan-Lucas Eickmann, Kai-Hong Luo, Mikhail Roiz, Jonas Lammers, Simone Atzeni, Cheeranjiv Pandey, Florian Lütkewitte, Reza G. Shirazi, Fabian Schlue, Benjamin Brecht, Vladimir V. Rybkin, Michael Stefszky, Christine Silberhorn
Simulating vibronic spectra is a central task in physical chemistry, offering insight into important properties of molecules. Recently, it has been experimentally demonstrated that photonic platforms based on Gaussian boson sampling (GBS) are capable of performing these simulations. However, whether an actual GBS approach is required depends on the molecule under investigation. To develop a better understanding on the requirements for simulating vibronic spectra, we explore connections between theoretical approximations in physical chemistry and their photonic counterparts. Mapping these approximations into photonics, we show that for certain molecules the GBS approach is unnecessary. We place special emphasis on the linear coupling approximation, which in photonics corresponds to sampling from multiple coherent states. By implementing this approach in experiments, we demonstrate improved similarities over previously reported GBS results for formic acid and identify the particular attributes that a molecule must exhibit for this, and other approximations, to be valid. These results highlight the importance in forming deeper connections between traditional methods and photonic approaches.
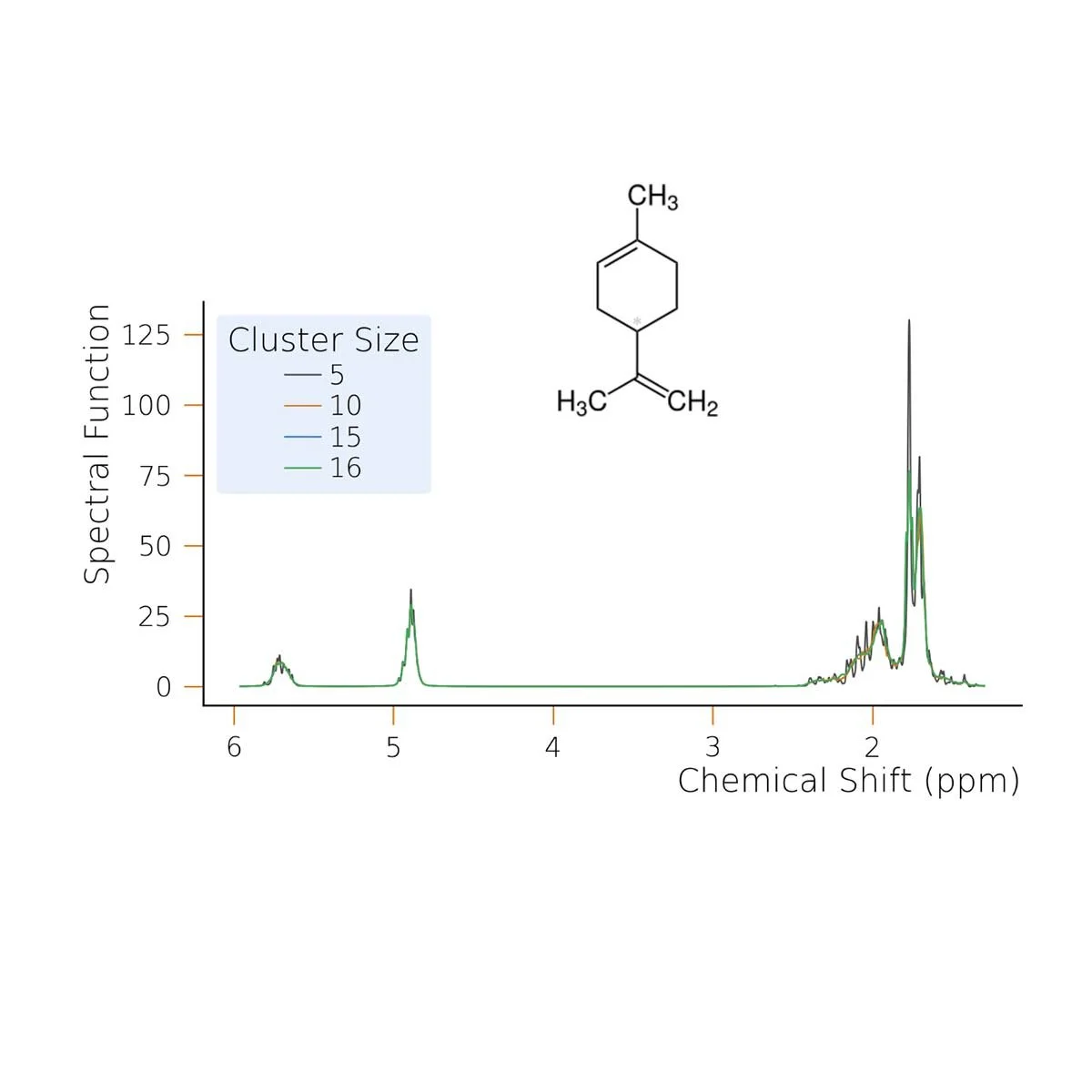
Can a Quantum Computer Simulate Nuclear Magnetic Resonance Spectra Better than a Classical One?
Authors: Keith R. Fratus, Nicklas Enenkel, Sebastian Zanker, Jan-Michael Reiner, Michael Marthaler, Peter Schmitteckert
The simulation of the spectra measured in nuclear magnetic resonance (NMR) spectroscopy experiments is a computationally non-trivial problem, and as such, it represents a problem for which a quantum computer may provide some practical advantage over traditional computing methods. In order to understand the extent to which such problems may provide examples of useful quantum advantage, it is important to understand the limitations of existing classical simulation methods. In this work, we benchmark our classical solver designed to solve such problems. We find that it performs well, even beyond the common experimental parameter regimes, except for a specific molecule with certain unusual features. We discuss what implications this may have for future efforts to demonstrate quantum advantage in the context of NMR.

White Paper: What is a good use case for quantum computers?
Authors: Michael Marthaler, Peter Pinski, Pascal Stadler, Vladimir Rybkin, Marina Walt
Identify, Transform, Benchmark, Show Quantum Advantage (ITBQ): Evaluating use cases for quantum computers. We introduce a four-step framework for assessing quantum computing applications -- from identifying relevant industry problems to demonstrating quantum advantage -- addressing steps often overlooked in the literature, such as rigorous benchmarking against classical solutions and the challenge of translating real-world tasks onto quantum hardware. Applying this framework to cases like NMR, multireference chemistry, and radicals reveals both significant opportunities and key barriers on the path to practical advantage. Our results highlight the need for transparent, structured criteria to focus research, guide investment, and accelerate meaningful quantum progress.
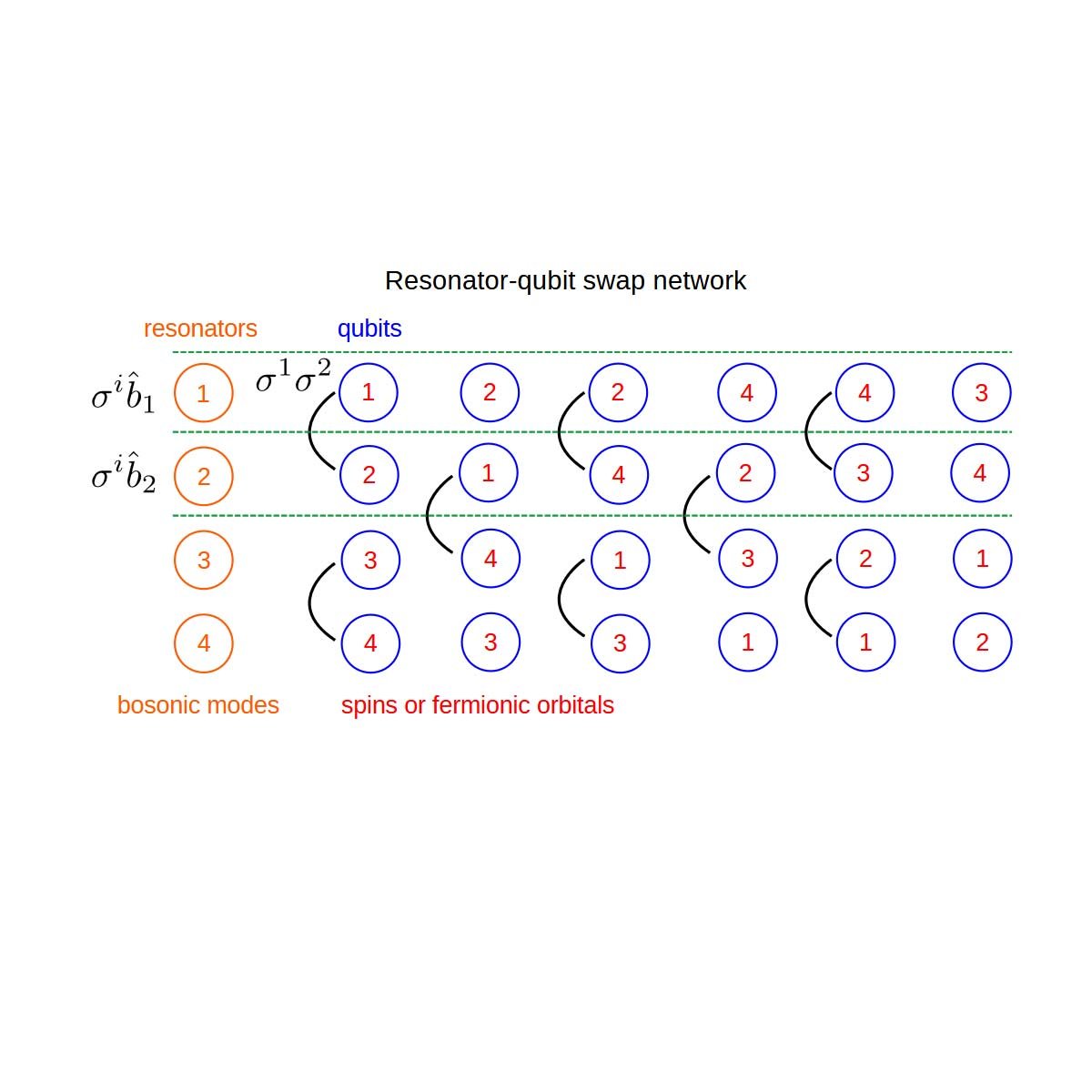
Quantum algorithms for simulating systems coupled to bosonic modes using a hybrid resonator-qubit quantum computer
Authors: Juha Leppäkangas, Pascal Stadler, Dmitry Golubev, Rolando Reiner, Jan-Michael Reiner, Sebastian Zanker, Nicola Wurz, Michael Renger, Jeroen Verjauw, Daria Gusenkova, Stefan Pogorzalek, Florian Vigneau, Ping Yang, William Kindel, Hsiang-Sheng Ku, Frank Deppe, Michael Marthaler
Modeling composite systems of spins or electrons coupled to bosonic modes is of significant interest for many fields of applied quantum physics and chemistry. A quantum simulation can allow for the solution of quantum problems beyond classical numerical methods. However, implementing this on existing noisy quantum computers can be challenging due to the mapping between qubits and bosonic degrees of freedom, often requiring a large number of qubits or deep quantum circuits. In this work, we discuss quantum algorithms to solve composite systems by augmenting conventional superconducting qubits with microwave resonators used as computational elements. This enables direct representation of bosonic modes by resonators. We derive efficient algorithms for typical models and propose a device connectivity that allows for feasible scaling of simulations with linear overhead. We also show how the dissipation of resonators can be a useful parameter for modeling continuous bosonic baths. Experimental results demonstrating these methods were obtained on the IQM Resonance cloud platform, based on high-fidelity gates and tunable couplers. These results present the first digital quantum simulation including a computational resonator on a commercial quantum platform.

Demonstration of system-bath physics on gate-based quantum computer
Authors: Pascal Stadler, Matteo Lodi, Andisheh Khedri, Rolando Reiner, Kirsten Bark, Nicolas Vogt, Michael Marthaler, and Juha Leppäkangas
We demonstrate algorithmic cooling on IBM-Q devices. We utilize inherent qubit noise to simulate the equilibration of an interacting spin system towards its ground state, when coupled to a dissipative auxiliary-spin bath. The steady-state correlations in the system are defined by the system Hamiltonian and are stable as long as the algorithm can be executed. In particular, we demonstrate the relaxation of system spins to ferromagnetic and antiferromagnetic ordering, controlled by the definition of the system Hamiltonian. We are able to perform simulated cooling for global systems of up to three system spins and four auxiliary spins.
A method to derive material-specific model descriptions of spin degrees of freedom coupled to a fermionic bath for materials displaying prevalent spin physics
Authors: Benedikt M. Schoenauer, Nicklas Enenkel, Florian G. Eich, Michael Marthaler, Sebastian Zanker, and Peter Schmitteckert
Magnetism and spin physics are true quantum mechanical effects and their description usually requires multi reference methods and is often hidden in the standard description of molecules in quantum chemistry. In this work we present a twofold approach to the description of spin physics in molecules and solids. First, we present a method that identifies the single-particle basis in which a given subset of the orbitals is equivalent to spin degrees of freedom for models and materials which feature significant spin physics at low energies. We introduce a metric for the spin-like character of a basis orbital, of which the optimization yields the basis containing the optimum spin-like basis orbitals. Second, we demonstrate an extended Schrieffer-Wolff transformation method to derive the effective Hamiltonian acting on the subspace of the Hilbert space in which the charge degree of freedom of electron densities in the spin-like orbitals is integrated out. The method then yields an effective spin-bath Hamiltonian description for the system. This extended Schrieffer-Wolff transformation is applicable to a wide range of Hamiltonians and has been utilized in this work for model Hamiltonians as well as the active space Hamiltonian of molecular chromium bromide.
Efficient Random Phase Approximation for Diradicals
Authors: Reza G. Shirazi, Vladimir V. Rybkin, Michael Marthaler, and Dmitry S. Golubev
We apply the analytically solvable model of two electrons in two orbitals to diradical molecules, characterized by two unpaired electrons. The effect of the doubly occupied and empty orbitals is taken into account by means of random phase approximation (RPA). We show that in the static limit the direct RPA leads to the renormalization of the parameters of the two-orbital model. We test our model by comparing its predictions for the singlet-triplet splitting with results from multi-reference CASSCF and NEVPT2 simulations for a set of ten molecules. We find that, for the whole set, the average relative difference between the singlet-triplet gaps predicted by the RPA-corrected two-orbital model and by NEVPT2 is about 40%. For the five molecules with the smallest singlet-triplet splitting the accuracy is better than 20%.
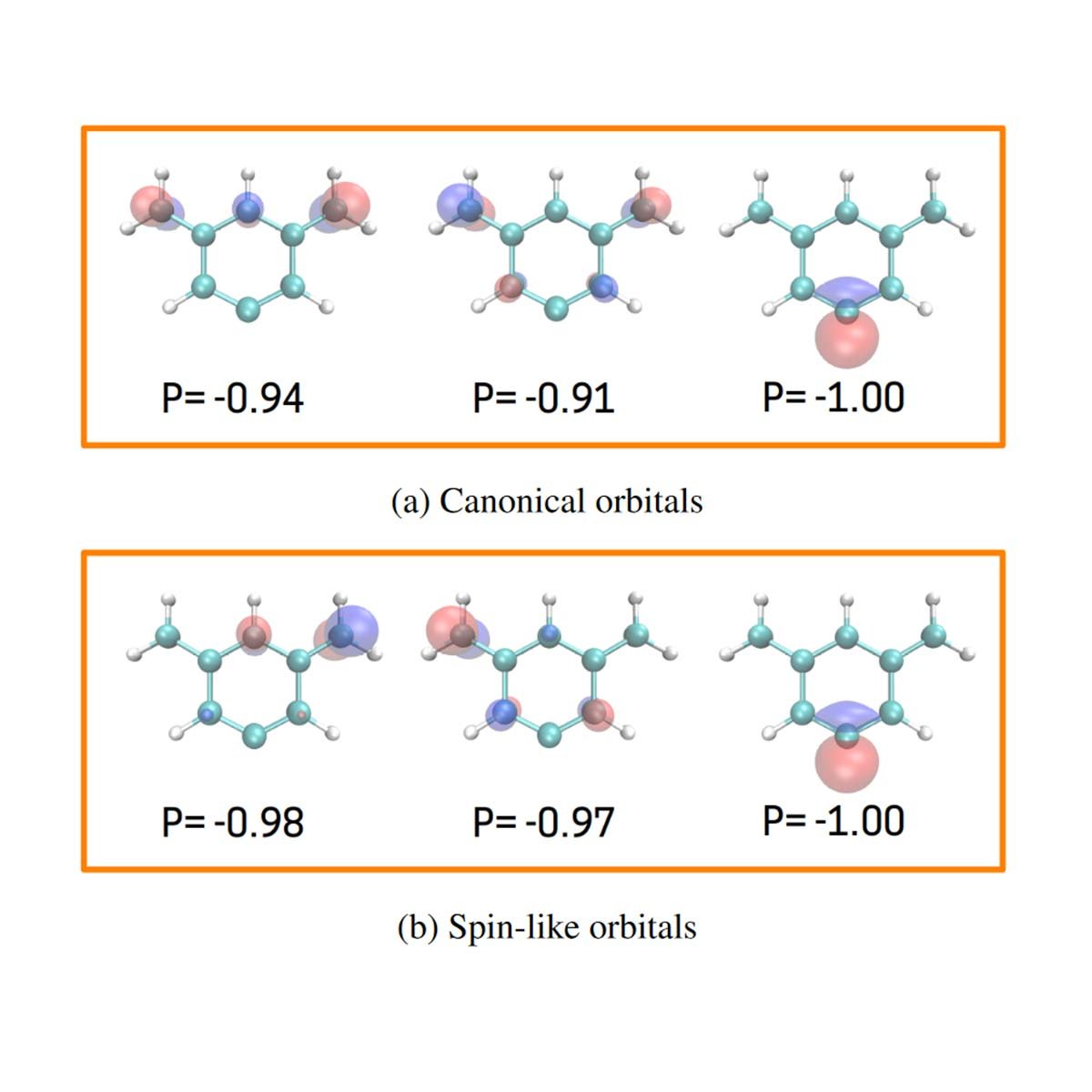
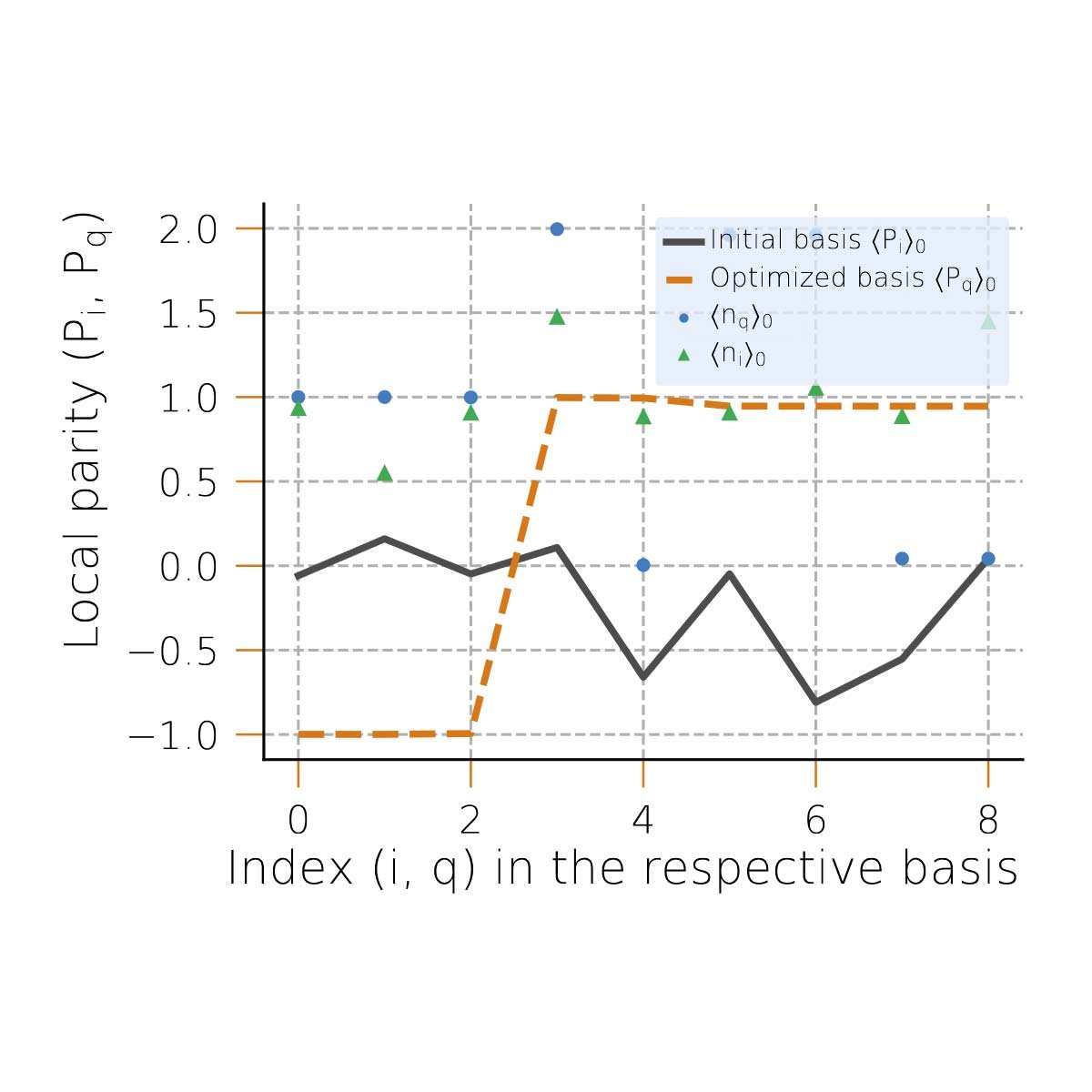
Understanding Radicals via Orbital Parities
Authors: Reza G. Shirazi, Benedikt M. Schoenauer, Peter Schmitteckert, Michael Marthaler, and Vladimir V. Rybkin
We introduce analysis of orbital parities as a concept and a tool for understanding radicals. Based on fundamental reduced one- and two-electron density matrices, our approach allows us to evaluate a total measure of radical character and provides spin-like orbitals to visualize real excess spin or odd electron distribution of singlet polyradicals. Finding spin-like orbitals aumotically results in their localization in the case of disjoint (zwitterionic) radicals and so enables radical classification based on spin-site separability. We demonstrate capabilities of the parity analysis by applying it to a number of polyradicals and to prototypical covalent bond breaking.
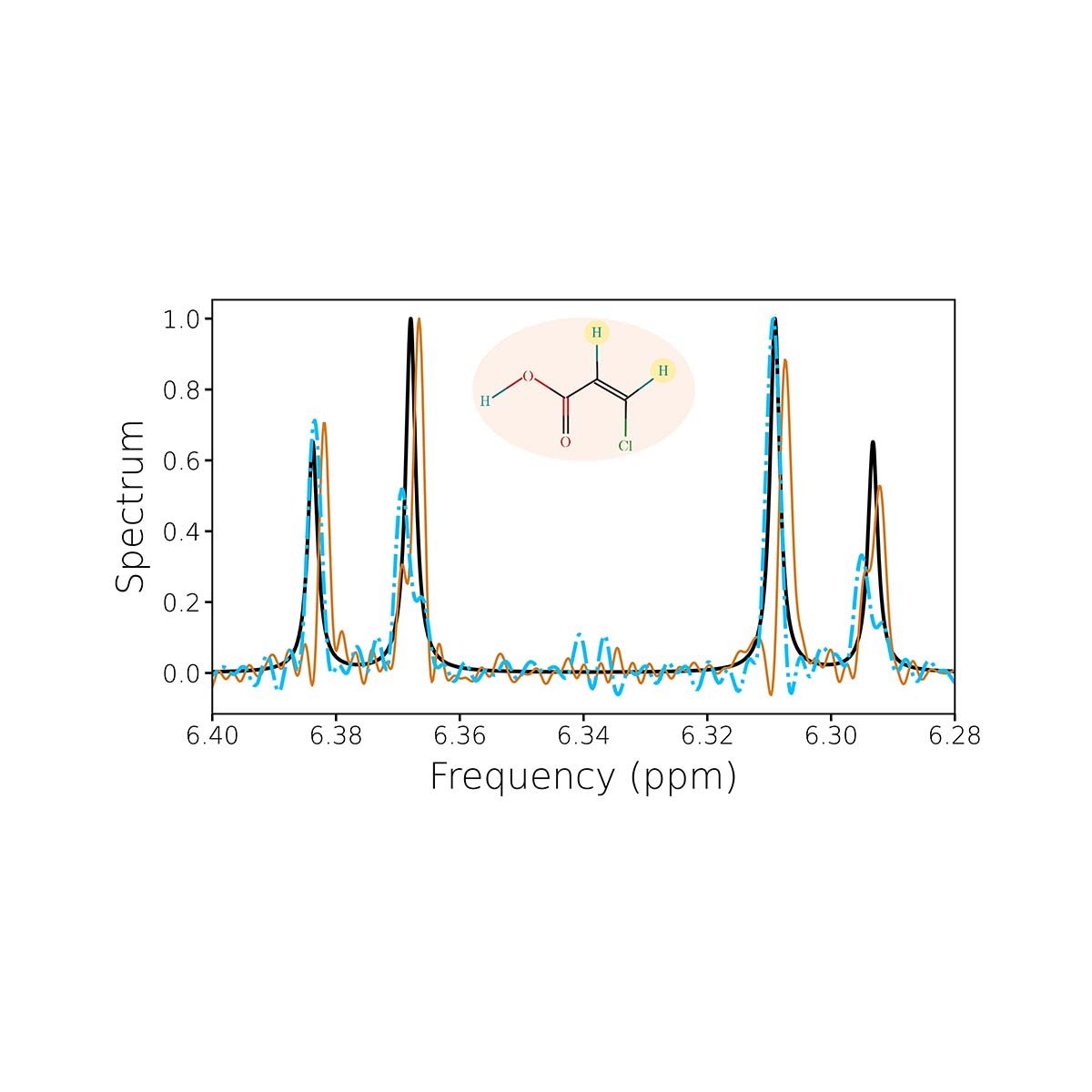
The impact of noise on the simulation of NMR spectroscopy on NISQ devices
Authors: Andisheh Khedri, Pascal Stadler, Kirsten Bark, Matteo Lodi, Rolando Reiner, Nicolas Vogt, Michael Marthaler, Juha Leppäkangas
We present the simulation of nuclear magnetic resonance (NMR) spectroscopy of small organic molecules with two promising quantum computing platforms, namely IBM's quantum processors based on superconducting qubits and IonQ's Aria trapped ion quantum computer addressed via Amazon Bracket. We analyze the impact of noise on the obtained NMR spectra, and we formulate an effective decoherence rate that quantifies the threshold noise that our proposed algorithm can tolerate. Furthermore we showcase how our noise analysis allows us to improve the spectra. Our investigations pave the way to better employ such application-driven quantum tasks on current noisy quantum devices.
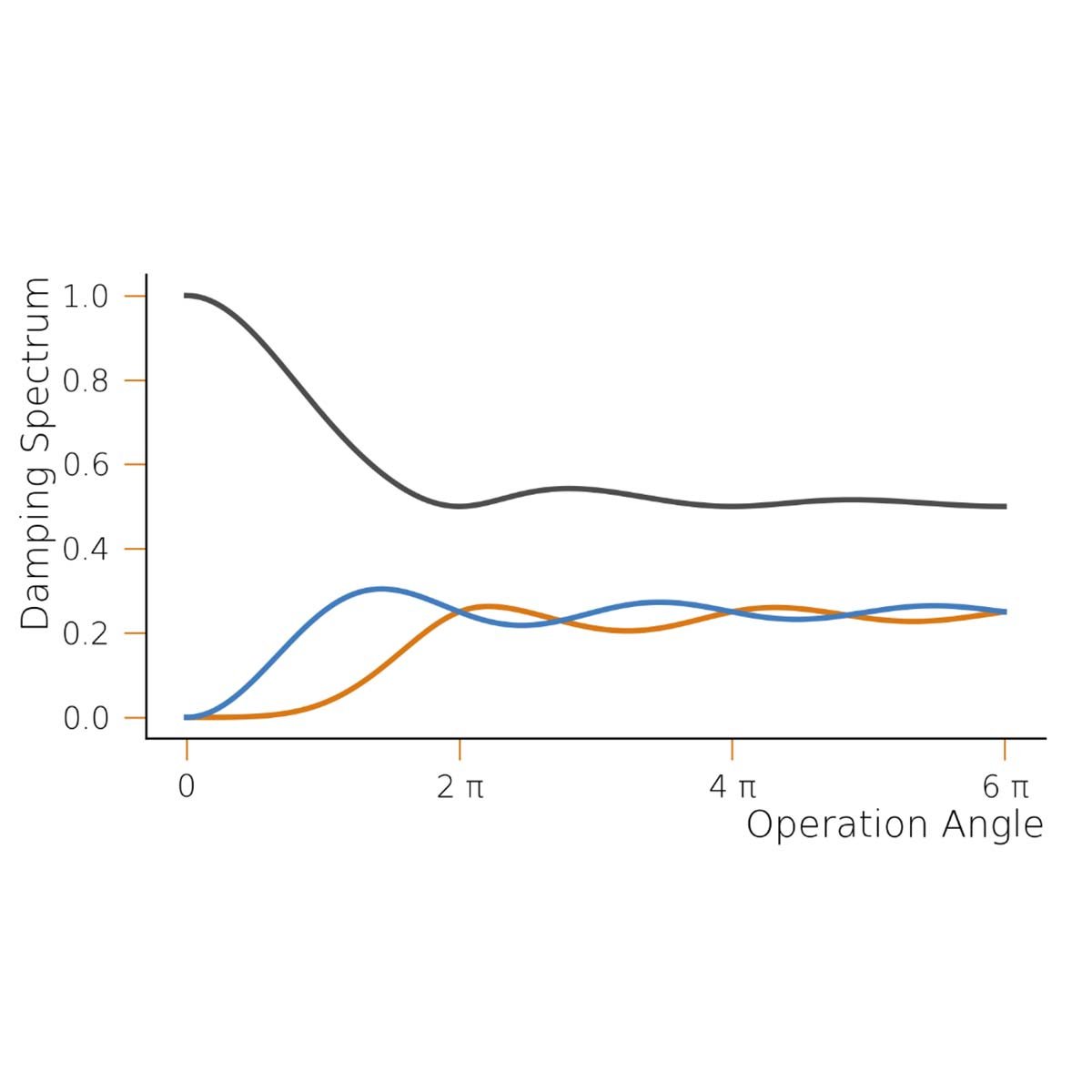
The Discrete Noise Approximation in Quantum Circuits
Authors: Keith R. Fratus, Juha Leppäkangas, Michael Marthaler, Jan-Michael Reiner
When modeling the effects of noise on quantum circuits, one often makes the assumption that these effects can be accounted for by individual decoherence events following an otherwise noise-free gate. In this work, we address the validity of this model. We find that under a fairly broad set of assumptions, this model of individual decoherence events provides a good approximation to the true noise processes occurring on a quantum device during the implementation of a quantum circuit. However, for gates that correspond to sufficiently large rotations of the qubit register, we find that the qualitative nature of these noise terms can vary significantly from the nature of the noise at the underlying hardware level. The bulk of our analysis is directed towards analyzing what we refer to as the separability ansatz, which is an ansatz concerning the manner in which individual quantum operations acting on a quantum system can be approximated. In addition to the primary motivation of this work, we identify several other areas of open research which may benefit from the results we derive here.
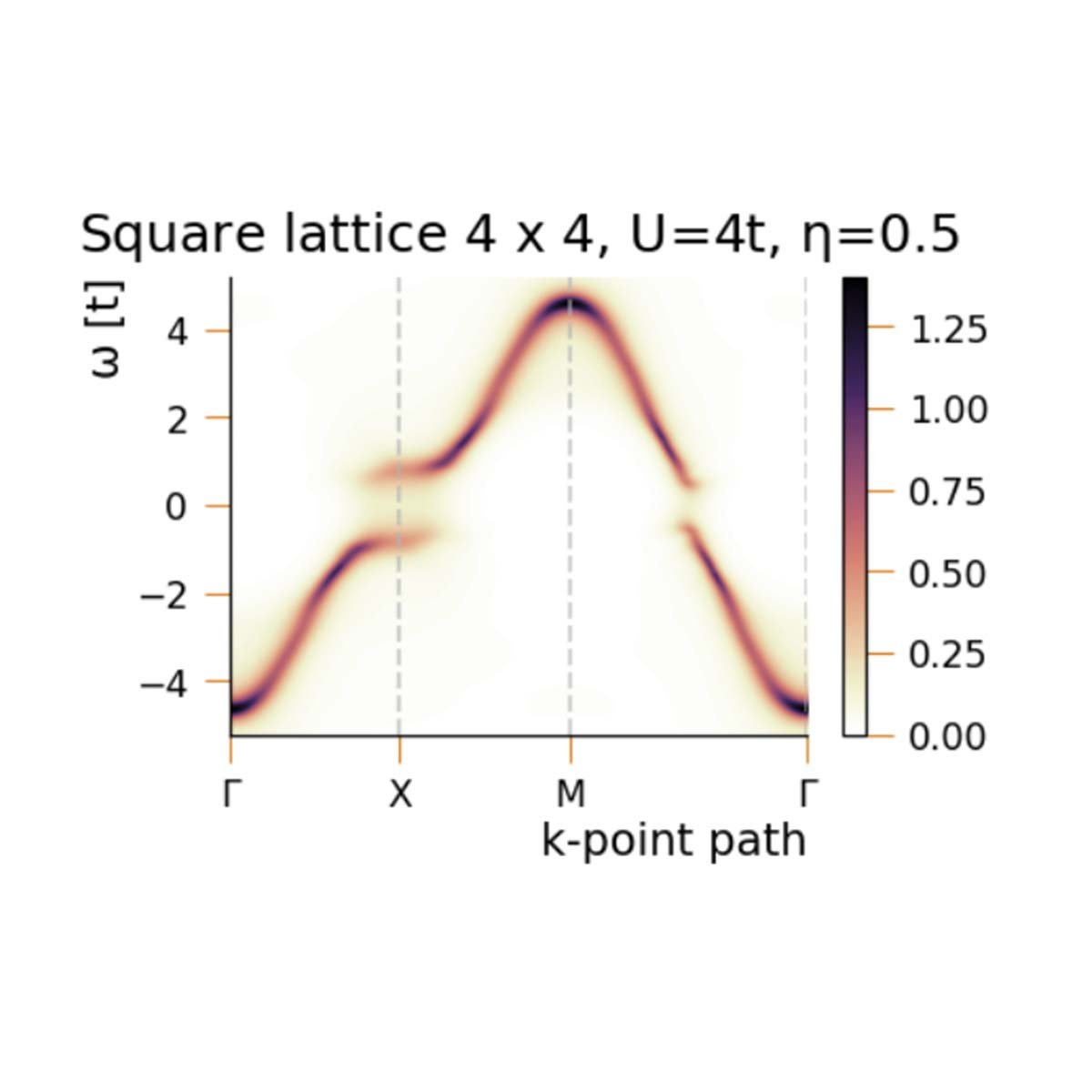
Applicability and limitations of cluster perturbation theory for Hubbard models
Authors: Nicklas Enenkel, Markus Garst, Peter Schmitteckert
Journal reference: Eur. Phys. J. Spec. Top. 10.1140, 2023
We present important use cases and limitations when considering results obtained from Cluster Perturbation Theory (CPT). CPT combines the solutions of small individual clusters of an infinite lattice system with the Bloch theory of conventional band theory in order to provide an approximation for the Green's function in the thermodynamic limit. To this end we are investigating single-band and multi-band Hubbard models in one- and two-dimensional systems. A special interest is taken in the supposed pseudo gap regime of the two-dimensional square lattice at half filling and intermediate interaction strength (U≤3t) as well as the metal-insulator transition. We point out that the finite-size level spacing of the cluster limits the resolution of spectral features within CPT. This restricts the investigation of asymptotic properties of the metal-insulator transition, as it would require much larger cluster sizes that are beyond computational capabilities.
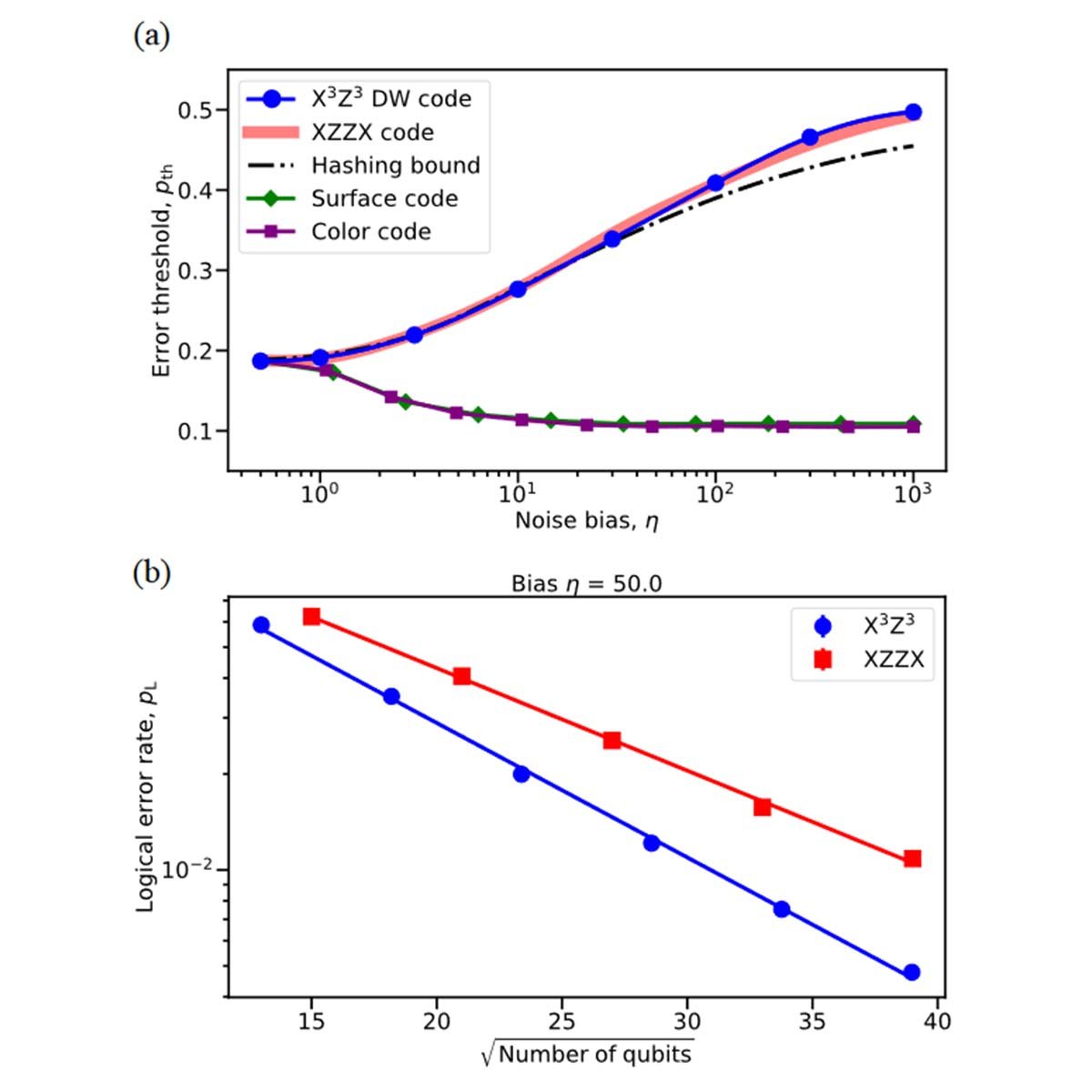
The domain wall color code
Authors: Konstantin Tiurev, Arthur Pesah, Peter-Jan H. S. Derks, Joschka Roffe, Jens Eisert, Markus S. Kesselring, Jan-Michael Reiner
We introduce the domain wall color code, a new variant of the quantum error-correcting color code that exhibits exceptionally high code-capacity error thresholds for qubits subject to biased noise. In the infinite bias regime, a two-dimensional color code decouples into a series of repetition codes, resulting in an error-correcting threshold of 50%. Interestingly, at finite bias, our color code demonstrates thresholds identical to those of the noise-tailored XZZX surface code for all single-qubit Pauli noise channels. The design principle of the code is that it introduces domain walls which permute the code's excitations upon domain crossing. For practical implementation, we supplement the domain wall code with a scalable restriction decoder based on a matching algorithm. The proposed code is identified as a comparably resource-efficient quantum error-correcting code highly suitable for realistic noise.

Post-processing noisy quantum computations utilizing N-representability constraints
Authors: Tomislav Piskor, Florian G. Eich, Michael Marthaler, Frank K. Wilhelm, Jan-Michael Reiner
We propose and analyze a method for improving quantum chemical energy calculations on a quantum computer impaired by decoherence and shot noise. The error mitigation approach relies on the fact that the one- and two-particle reduced density matrices (1- and 2-RDM) of a chemical system need to obey so-called N-representability constraints. We post-process the result of an RDM measurement by projecting it into the subspace where certain N-representability conditions are fulfilled. Furthermore, we utilize that such constraints also hold in the hole and particle-hole sector and perform projections in these sectors as well. We expand earlier work by conducting a careful analysis of the method's performance in the context of quantum computing. Specifically, we consider typical decoherence channels (dephasing, damping, and depolarizing noise) as well as shot noise due to a finite number of projective measurements. We provide analytical considerations and examine numerically three example systems, \ch{H2}, \ch{LiH}, and \ch{BeH2}. From these investigations, we derive our own practical yet effective method to best employ the various projection options. Our results show the approach to significantly lower energy errors and measurement variances of (simulated) quantum computations.
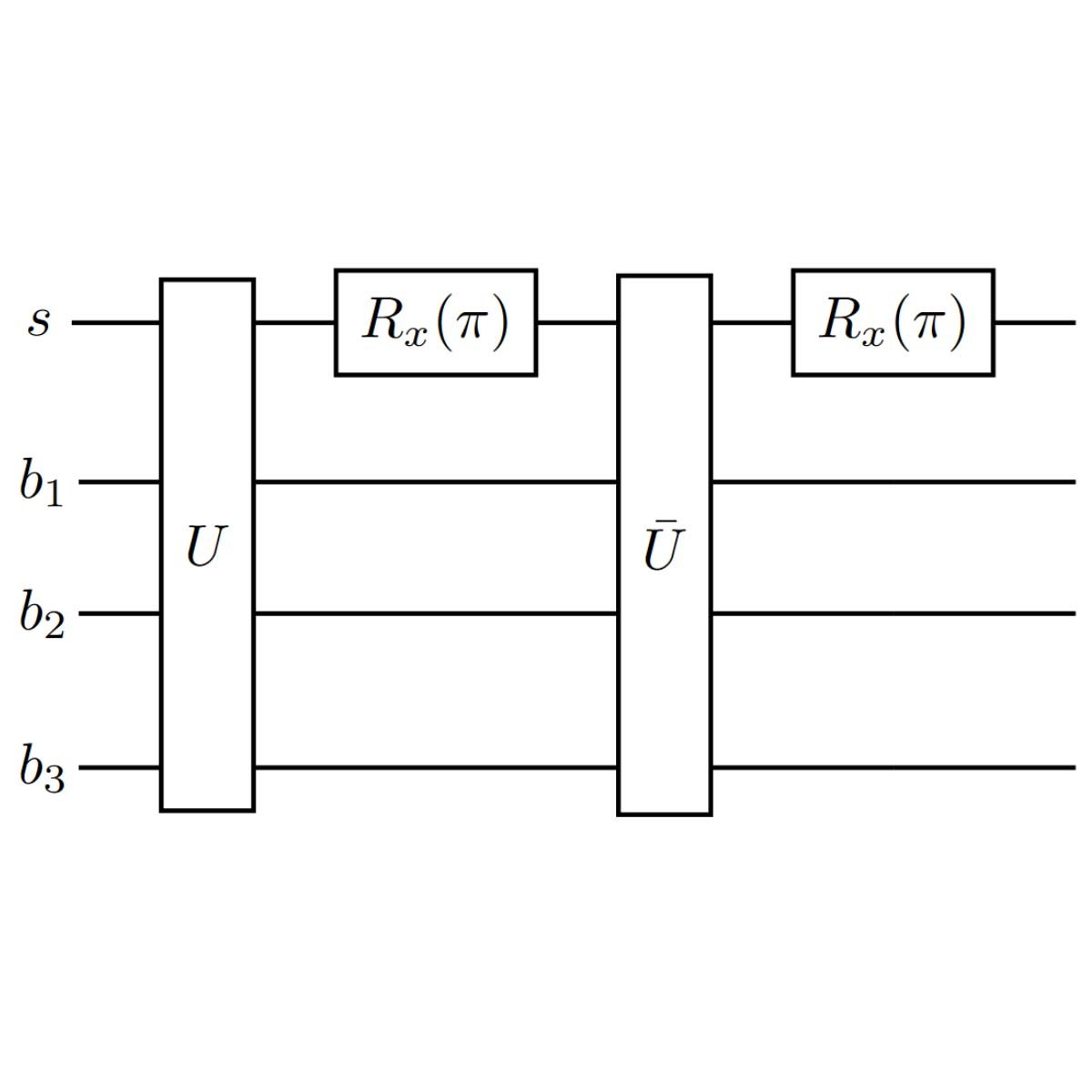
A quantum algorithm for solving open system dynamics on quantum computers using noise
Authors: Juha Leppäkangas, Nicolas Vogt, Keith R. Fratus, Kirsten Bark, Jesse A. Vaitkus, Pascal Stadler, Jan-Michael Reiner, Sebastian Zanker, Michael Marthaler
In this paper, we present a quantum algorithm that uses noise as a resource. The goal of our quantum algorithm is the calculation of operator averages of an open quantum system evolving in time. Selected low-noise system qubits and noisy bath qubits represent the system and the bath of the open quantum system. All incoherent qubit noise can be mapped to bath spectral functions. The form of the spectral functions can be tuned digitally, allowing for the time evolution of a wide range of open-system models at finite temperatures. We study the feasibility of this approach with a focus on the solution of the spin-boson model and assume intrinsic qubit noise that is dominated by damping and dephasing. We find that classes of open quantum systems exist where our algorithm performs very well, even with gate errors as high as 1%. In general, the presented algorithm performs best if the system-bath interactions can be decomposed into native gates.
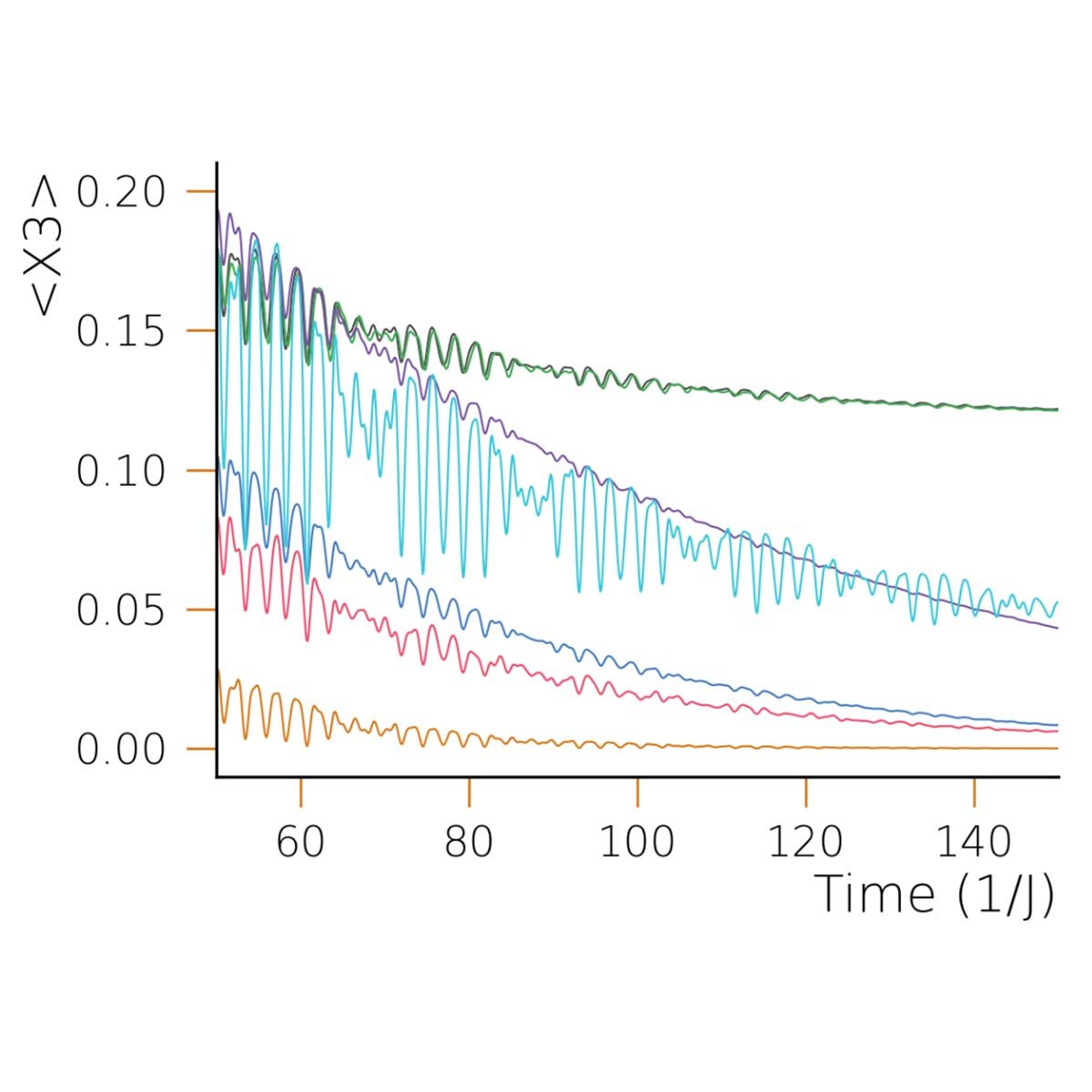
Describing Trotterized Time Evolutions on Noisy Quantum Computers via Static Effective Lindbladians
Authors: Keith R. Fratus, Kirsten Bark, Nicolas Vogt, Juha Leppäkangas, Sebastian Zanker, Michael Marthaler, Jan-Michael Reiner
We consider the extent to which a noisy quantum computer is able to simulate the time evolution of a quantum spin system in a faithful manner. Given a specific set of assumptions regarding the manner in which noise acting on such a device can be modeled at the circuit level, we show how the effects of noise can be reinterpreted as a modification to the dynamics of the original system being simulated. In particular, we find that this modification corresponds to the introduction of static Lindblad noise terms, which act in addition to the original unitary dynamics. The form of these noise terms depends not only on the underlying noise processes occurring on the device but also on the original unitary dynamics, as well as the manner in which these dynamics are simulated on the device, i.e., the choice of a quantum algorithm. We call this effectively simulated open quantum system the noisy algorithm model. Our results are confirmed through numerical analysis.
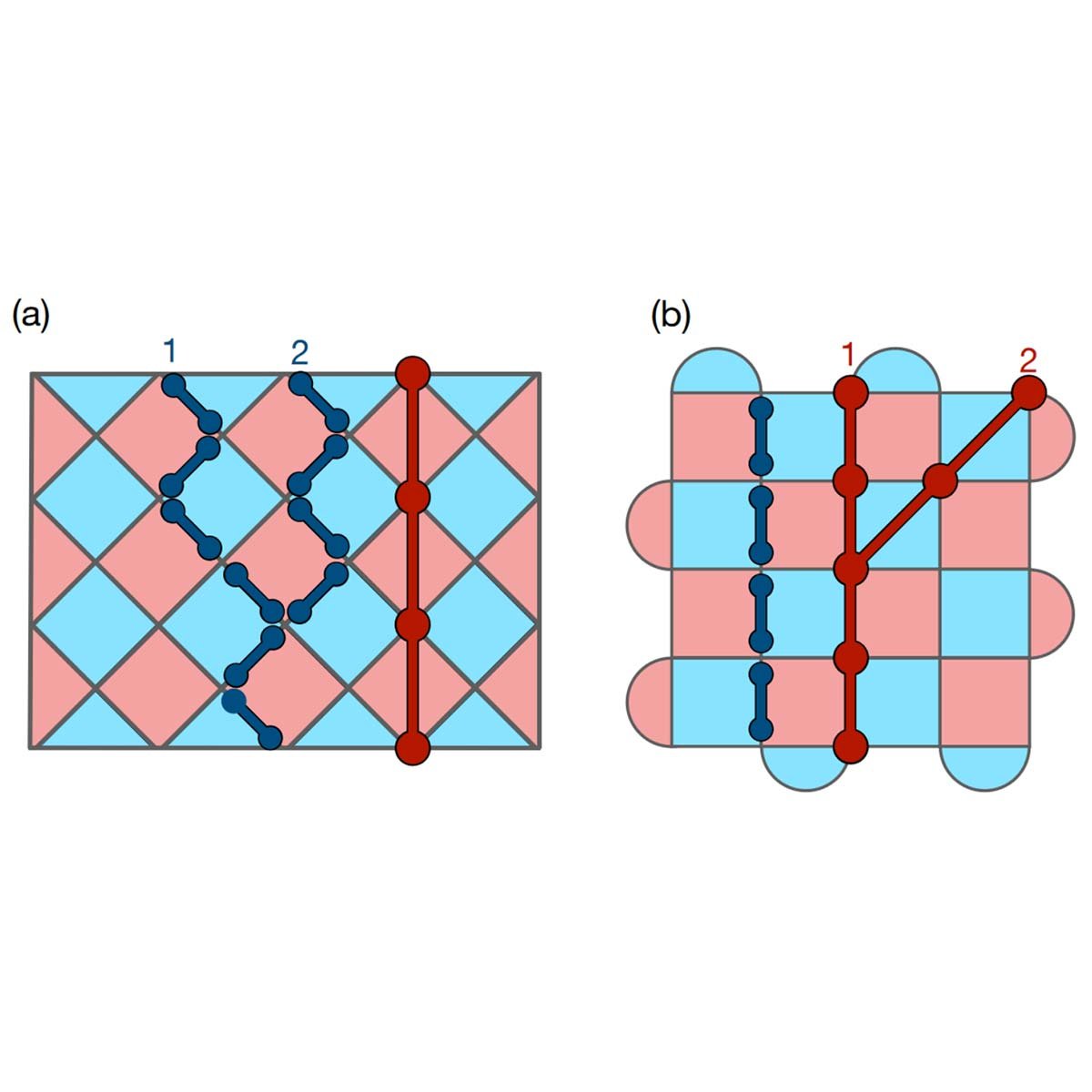
Correcting non-independent and non-identically distributed errors with surface codes
Authors: Konstantin Tiurev, Peter-Jan H. S. Derks, Joschka Roffe, Jens Eisert, Jan-Michael Reiner
Journal reference: Quantum 7, 1123 (2023)
A common approach to studying the performance of quantum error correcting codes is to assume independent and identically distributed single-qubit errors. However, the available experimental data shows that realistic errors in modern multi-qubit devices are typically neither independent nor identical across qubits. In this work, we develop and investigate the properties of topological surface codes adapted to a known noise structure by Clifford conjugations. We show that the surface code locally tailored to non-uniform single-qubit noise in conjunction with a scalable matching decoder yields an increase in error thresholds and exponential suppression of sub-threshold failure rates when compared to the standard surface code. Furthermore, we study the behaviour of the tailored surface code under local two-qubit noise and show the role that code degeneracy plays in correcting such noise. The proposed methods do not require additional overhead in terms of the number of qubits or gates and use a standard matching decoder, hence come at no extra cost compared to the standard surface-code error correction.

Spectral Function of the 2D Hubbard Model Studied with Cluster Perturbation Theory
Master’s Thesis of Nicklas Enenkel at the Institute of Theoretical Solid State Physics, Karlsruhe Institute of Technology
The study examines the single-band Hubbard model on a cubic lattice at half-filling, focusing on the pseudogap in two-dimensional systems with intermediate interaction strength (U ≤ 3t) and the metal-insulator transition. Using Cluster Perturbation Theory (CPT), the authors approximate the Green’s function from small clusters. They validate the method with the 1D model, finding that CPT's resolution is limited by cluster size and yields unreliable results at intermediate U. The observed pseudogap at U = 4t is deemed an artifact of the approximation. The authors suggest future work to overcome computational limitations and improve CPT interpretations.

Using gradient-based algorithms to determine ground state energies on a quantum computer
Authors: Tomislav Piskor, Florian G. Eich, Jan-Michael Reiner, Sebastian Zanker, Nicolas Vogt, Michael Marthaler, Frank Wilhelm-Mauch
Journal reference: Phys. Rev. A 105, 062415 – Published 8 June 2022
Variational algorithms are promising candidates to be implemented on near-term quantum computers. The variational quantum eigensolver (VQE) is a prominent example, where a parametrized trial state of the quantum mechanical wave function is optimized to obtain the ground state energy. In our work, we investigate the variational Hamiltonian Ansatz (VHA), where the trial state is given by a non-interacting reference state modified by unitary rotations using generators that are part of the Hamiltonian describing the system. The lowest energy is obtained by optimizing the angles of those unitary rotations. A standard procedure to optimize the variational parameters is to use gradient-based algorithms. However, shot noise and the intrinsic noise of the quantum device affect the evaluation of the required gradients. We studied how different methods for obtaining the gradient, specifically the finite-difference and the parameter-shift rule, are affected by shot noise and noise of the quantum computer. To this end, we simulated a simple quantum circuit, as well as the 2-site and 6-site Hubbard model.
